I. Le calcul économique du consommateur
Dans l'approche microéconomique des choix de consommation, le consommateur est un agent économique rationnel, il effectue des calculs en comparant les prix et les quantités disponibles afin de constituer le panier de consommation qui va lui procurer la satisfaction la plus élevée.
Il dispose d'un revenu fixe qu'il dépense intégralement en opérant des choix entre deux ou plusieurs biens, choix guidés par ses préférences, elles-mêmes liées à l'utilité retirée de la consommation des différents biens. L'objectif du consommateur est de maximiser son utilité compte tenu de sa contrainte de budget.
Le choix du consommateur porte sur des paniers de consommation. pour simplifier l’analyse, on raisonne généralement sur des paniers constitués de deux biens. Le panier X se note (x1, x2), x1 représentant la quantité de bien 1 que le consommateur décide d’acheter. C'est le concept abstrait de préférence qui permet d'ordonner les différents paniers de biens. On estime que :
- Tout consommateur rationnel est ainsi capable de dire s’il préfère tel panier de bien à tel autre ou s’il lui est indifférent de consommer l’un ou l’autre des deux paniers.
- Du fait d’une hypothèse de non satiété, un consommateur préfère toujours consommer plus. Tout panier de biens comportant une quantité supérieure de l’un des deux biens, à quantité égale du second, sera ainsi préféré au premier. Cependant, le consommateur ayant également une préférence pour la diversité, il consommera toujours des deux biens.
C’est le concept d’utilité qui permet de mesurer la satisfaction que retire le consommateur de la consommation d'un panier de biens. Le niveau de l’utilité dépend donc de la quantité consommée (Q) et peut être formalisé à l’aide d’une fonction d’utilité : U = f (Q) = f (x1, x2). Cette fonction indique ainsi le niveau d’utilité d’un consommateur donné lorsqu’il acquiert les quantités x1 et x2 des biens 1 et 2.
C’est à partir de la fonction d’utilité que l’on construit les courbes d’indifférence du consommateur, grâce à une représentation graphique pour des biens substituables.
Une courbe d’indifférence représente l’ensemble des paniers de consommation qui procurent la même utilité au consommateur : on parle également de courbe d’iso-utilité.
Il existe, pour un même individu, plusieurs courbes d’indifférence qui représentent chacune un niveau de satisfaction différent.
On peut ainsi caractériser la forme des courbes d’indifférence :
- Une courbe d’indifférence est continue, décroissante, et convexe.
- Si le consommateur préfère un panier à un autre, il éprouve une satisfaction plus importante : dès lors, la courbe d’indifférence est donc plus élevée que la précédente. Plus ces courbes sont éloignées de l’origine du graphique, plus elles correspondent à des niveaux de satisfaction et d’utilité élevés.
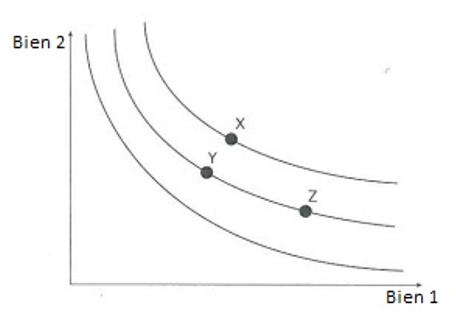
Dans cet exemple (courbe d’indifférence pour des biens substituables), le panier X est préféré aux paniers Y et Z, car il est situé sur une courbe d’indifférence représentant un niveau d’utilité plus élevé.
Les paniers Y et Z procurent le même degré de satisfaction au consommateur. On dit qu’il est indifférent à l’égard de ces deux paniers.
Le long d'une courbe d'indifférence, pour maintenir une utilité constante, le consommateur doit renoncer à une certaine quantité d'un des deux biens pour pouvoir consommer une quantité supplémentaire de l'autre bien.
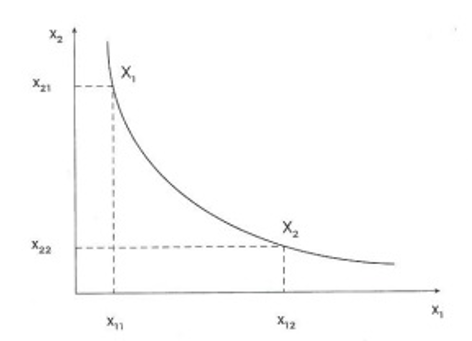
Ainsi, dans le passage de X1 à X2, il a dû accepter de renoncer à la quantité (x21 – x22) de bien 2, en échange d’une augmentation (x11 + x12) de la quantité de bien 1.
Le taux auquel le consommateur est disposé à substituer une quantité de bien 2 au bien 1 est appelé taux marginal de substitution (TMS) entre les biens 1 et 2. Ce TMS est égal au rapport des utilités marginales des deux biens.
Les préférences du consommateur ne vont pas pouvoir entièrement guider ses choix. En effet, ceux-ci sont limités par une contrainte imposée par son revenu et le prix des biens.
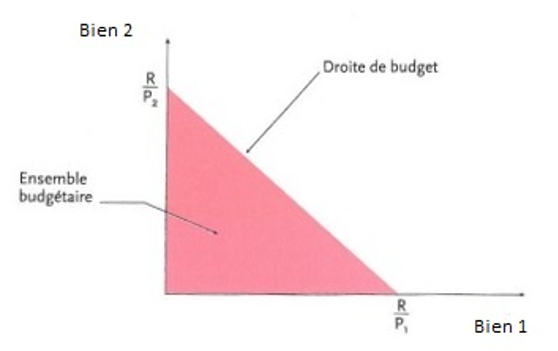
L’ensemble budgétaire du consommateur est alors constitué par les paniers accessibles pour des prix p1 et p2 (prix unitaires respectifs des deux biens, fixés par le marché) et un revenu R donné, intégralement dépensé. La contrainte de budget marque la frontière de cet ensemble budgétaire et est formalisée par la relation :
p1 x1 + p2 x2 = R
p1x1 représente la dépense en bien 1. Elle est représentée par une droite, dont on peut écrire l'équation sous la forme :
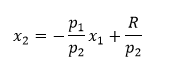
L’ordonnée à l’origine (qui mesure la quantité maximale de bien 2 que l'on peut consommer si l'on dépense la totalité de son revenu dans l'achat de ce bien) est égale à Rp2 et la pente de la droite de budget est donnée par le rapport -p1p2
, c’est-à-dire l’opposé du rapport des prix des deux biens : si le consommateur dépense une unité monétaire de plus pour consommer du bien 1, il devra réduire sa dépense en bien 2 (on parle également de coût d’opportunité de la consommation du bien 1).
Un accroissement du revenu, toutes choses égales par ailleurs (à prix des biens inchangés) accroît l’ordonnée à l’origine Rp2 mais n’affecte pas la pente de la droite (elle est indépendante de R).
Une augmentation (baisse) du revenu se traduit donc par un déplacement parallèle et vers le haut (bas) de la droite de budget.
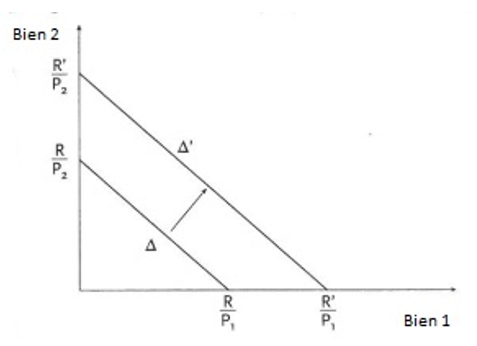
Les prix p1 et p2 étant fixés, le passage de Δ à Δ’ traduit une augmentation du revenu et donc une augmentation du pouvoir d’achat du consommateur.
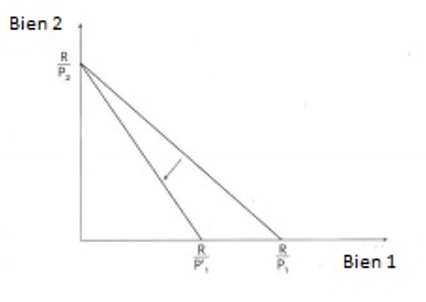
Un accroissement du prix p1, « toutes choses égales par ailleurs » (p2 et R inchangés) ne modifie pas l’ordonnée à l’origine mais accroît (en valeur absolue) la pente de la droite de budget. Celle-ci « pivote » alors autour de l’ordonnée à l’origine.
L’équilibre du consommateur est le panier de consommation, traditionnellement nommé X*, qui rend maximale la fonction d’utilité tout en étant compatible avec la contrainte de budget.
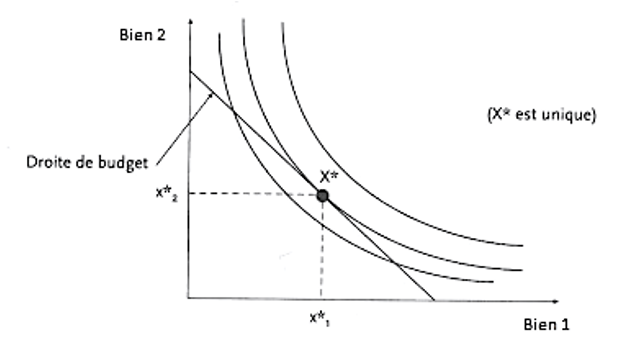
Le panier (x*1, x*2) constitue le choix optimal du consommateur. Il faut en effet choisir un point situé sur la droite de budget. Il en existe une infinité. Tant qu’il y a deux points d’intersection entre une courbe d’indifférence et la droite de budget, il existe une courbe d’indifférence située plus haut qui reste accessible au consommateur.
Le point optimal (X*) est le point de la droite de budget qui n’a plus qu’un point de tangence avec une courbe d’indifférence.
Ainsi, le consommateur se trouve à l’équilibre lorsque, pour un budget donné, des prix de biens de consommation déterminés, son niveau d’utilité est le plus élevé possible.
L’équilibre est donc une situation de laquelle le consommateur n’a pas intérêt à s’éloigner.
II. Le calcul économique du producteur
On appelle facteurs de production (ou inputs) tous les éléments nécessaires à la production d’un bien ou d’un service (ou output) et utilisés dans le processus de production. Ces facteurs de production sont combinés ensemble pour donner un produit.
Les facteurs de production sont substituables ou complémentaires :
- Ils sont substituables s’il est possible de substituer une quantité donnée d’un facteur de production par une quantité donnée d’un autre facteur, tout en conservant le même niveau de production.
- Deux facteurs sont complémentaires lorsqu’une quantité donnée d’un facteur ne peut être associée qu’à une quantité fixe d’un autre.
La nature impose aux entreprises des contraintes techniques : l’ensemble de toutes les combinaisons d’inputs et d’outputs qui correspondent à un processus de production techniquement réalisable est appelé un ensemble de production.
La fonction de production indique le niveau maximal de production qui peut être obtenu par les différentes combinaisons de facteurs de production, la technologie étant donnée.
On suppose qu’il n’y a que deux facteurs de production : travail (L) et capital (K). Q représente la quantité produite du bien considéré, K et L sont les quantités respectivement de travail et de capital. Les facteurs de production sont supposés substituables.
On écrit ainsi la fonction de production F :
Q = F (K, L)
Pour mesurer l’efficacité de la production, la notion de productivité est essentielle :
- La productivité marginale (Pm) d’un facteur de production est le supplément de production découlant de l’utilisation d’une unité supplémentaire de ce facteur, la quantité de l’autre restant fixe. On suppose généralement que cette productivité marginale est positive et décroissante.
- La productivité moyenne (PM) de chacun des facteurs représente les quantités produites par unité de facteur de production : la productivité moyenne d’un facteur de production est le rapport de la production totale Q à la quantité employée de ce facteur (Q/K ou Q/L).
La théorie microéconomique utilise pour la théorie du producteur un cadre analytique analogue à celui de la théorie du consommateur avec les courbes d’indifférence.
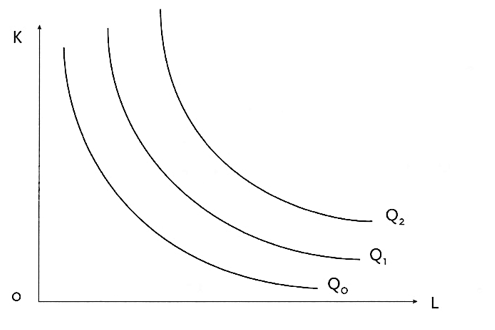
Une isoquante (ou courbe d’isoproduit) est ainsi une courbe indiquant l’ensemble des combinaisons de capital (K) et de travail (L) qui, pour un état donné des techniques, permettent de produire une même quantité (Q). Il y a une infinité d’isoquantes, chacune correspondant à un niveau de production différent, qui va en s’accroissant lorsqu’on se déplace vers le haut.
- Plus l’isoquante est située en haut à droite du graphique, plus elle correspond à un niveau de production élevé.
- Une isoquante est décroissante (hypothèse de productivité marginale positive des facteurs de production), et convexe (la difficulté de la substitution s’accroît avec la substitution).
Le taux marginal de substitution technique (TMST) est le taux auquel on peut échanger les facteurs de production (K, L), tout en conservant le même niveau de production. En un point d’une isoquante, le TMST est égal à l’opposé de la pente de la tangente à l’isoquante en ce point. Il est égal au rapport des productivités marginales des deux facteurs de production.
Si l’on appelle D la dépense que le producteur affecte à l’achat des facteurs de production (travail et capital), w le prix du facteur travail et r le prix du facteur capital, on peut écrire la contrainte de budget du producteur de la façon suivante :
D = w L + r K
L’équation de la droite d’isocoût est donc celle d’une droite dont la pente est égale à l’opposé du rapport des prix des facteurs de production.
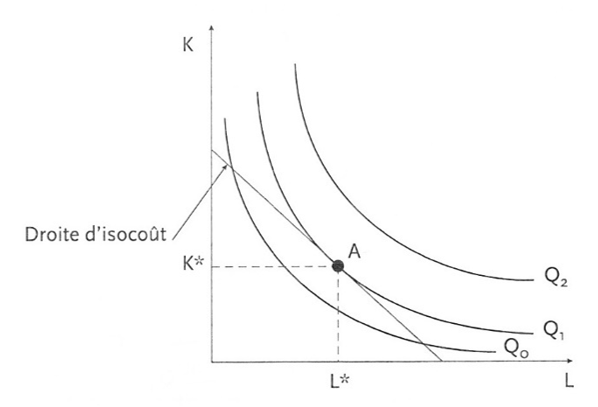
Le producteur qui veut atteindre un niveau de production donné minimise ses coûts lorsqu’il choisit la combinaison productive (combinaison de facteurs K et L) qui se trouve au point de tangence entre l’isoquant considéré et une droite d’isocoût.
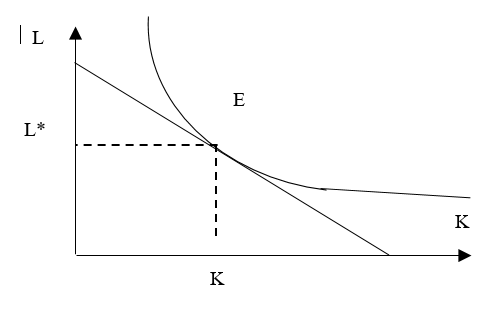
De la même façon que pour la théorie du consommateur, on peut montrer qu’à l’équilibre du producteur, le TMST (égal au rapport des productivités marginales des facteurs) est égal au rapport des prix des facteurs de production.
L’équilibre est atteint lorsque l’isoquante est tangente à l’isocoût, donc les deux pentes des deux courbes sont égales.
On peut ainsi raisonner sur l’équilibre du producteur à court terme.
Le producteur est en situation d’équilibre lorsqu’il maximise son profit : à ce niveau, il n’a plus aucun intérêt à modifier sa décision.
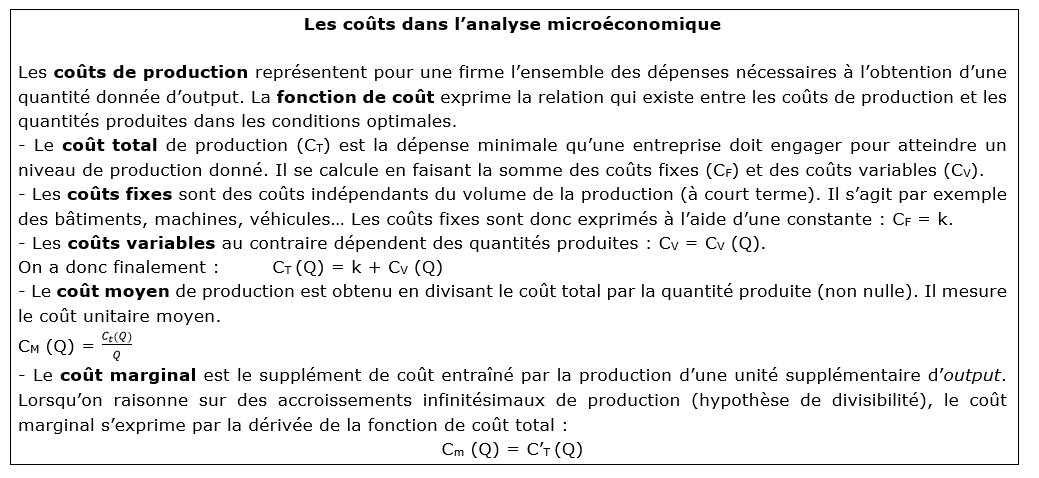
Le profit du producteur π est la différence entre son chiffre d’affaires (produit des quantités vendues Q par le prix de vente p de sa marchandise : P.Q) et le niveau des coûts C.
En concurrence pure et parfaite, le prix est donné par le marché. La recette moyenne du producteur est égale au prix de vente du produit.
En effet, la recette totale (RT) est telle que RT (Q) = P x Q, et donc la recette moyenne est égale à :
RM(Q) = Rt(Q)Q=P×QQ=P
Comme en concurrence pure et parfaite, une unité supplémentaire de bien ne peut qu’être vendue au prix unitaire de ce bien, la recette marginale est aussi égale au prix.
Par ailleurs, pour que le producteur maximise son profit, il faut donc que la productivité marginale de chaque facteur soit égale à son prix : en effet, le producteur a intérêt à augmenter l’utilisation d’un facteur de production tant que le supplément de recettes permis par l’utilisation d’une unité supplémentaire de ce facteur est supérieur à son coût.
On a donc : RM (Q) = Rm (Q) = P
Le profit (π) est tel que : π(Q) = P x Q – CT(Q)
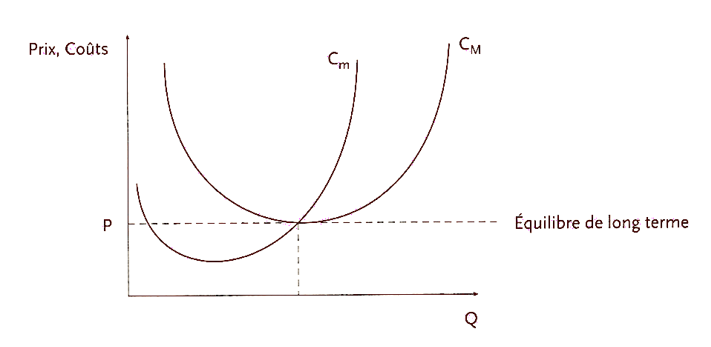
Ainsi, pour maximiser son profit, le producteur doit vendre une quantité telle que : Cm = P, et donc telle que : Cm = Rm
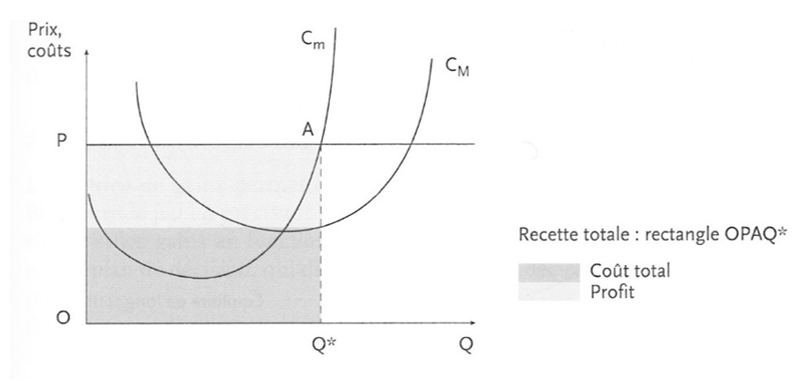
L’équilibre à long terme
À long terme, les perspectives de profit attirent de nouvelles firmes sur le marché. Ces nouveaux arrivants utilisent la meilleure technique de production et les fonctions de coûts sont alors identiques pour toutes les entreprises. L’accroissement de l’offre provoque une baisse du prix de marché et donc du profit économique, jusqu’au niveau du seuil de rentabilité (minimum du coût moyen). À ce niveau, le profit économique (profit global) est nul et il n’y a donc plus d’incitation à entrer sur le marché.